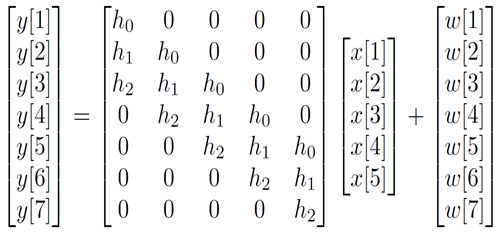
估计x，H已知，\(\mathbf{w} \sim \mathcal{N}\left(\mathbf{0}, \mathbf{I}_{w}\right)\)

方法：ML

我们知道对于向量\(x=[x_1,x_2]^T,x_1,x_2 \sim N(\mu, \sigma^2)\) \(p(x)=\frac{1}{(2 \pi)^{\frac{n}{2}} \operatorname{det} \frac{1}{2}(C)} \exp \left[-\frac{1}{2}(x-\mu)^{T} C^{-1}(x-\mu)\right]\)

当w满足 \(\mathbf{w} \sim \mathcal{N}\left(\mathbf{0}, \mathbf{I}_{w}\right)\) \(p(\mathbf{y} \mid \mathbf{H} \mathbf{x})=\frac{1}{(2 \pi)^{N / 2} \sqrt{\operatorname{det}\left(\mathbf{I}_{w}\right)}} \exp \left(-\frac{1}{2}(\mathbf{y}-\mathbf{H} \mathbf{x})^{H} \mathbf{I}_{w}^{-1}(\mathbf{y}-\mathbf{H x})\right)\)