一个任意函数总能表示成一个奇函数+一个偶函数的形式：

\[\begin{array}{l} f(x)=\frac{f(x)+f(-x)}{2}+\frac{f(x)-f(x)}{2} \\ \text { 令 }\left\{\begin{array}{l} g(x)=f_{e}(x)=Ev(f(x))=\frac{f(x)+f(-x)}{2} \\ h(x)=f_{o}(x)=Od(f(x))=\frac{f(x)-f(-x)}{2} \end{array}\right. \end{array}\]

Ev即偶分量，Od即奇分量。

MIT 6-007 signals and systems 2-5

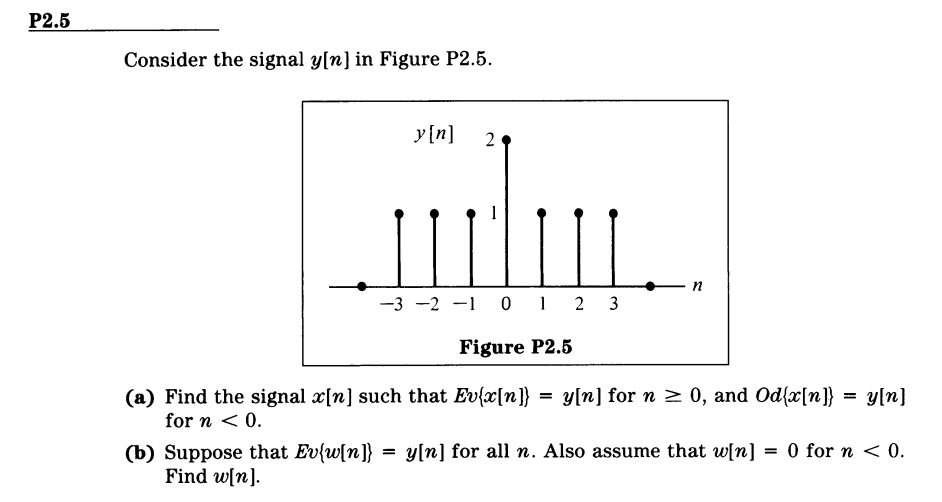
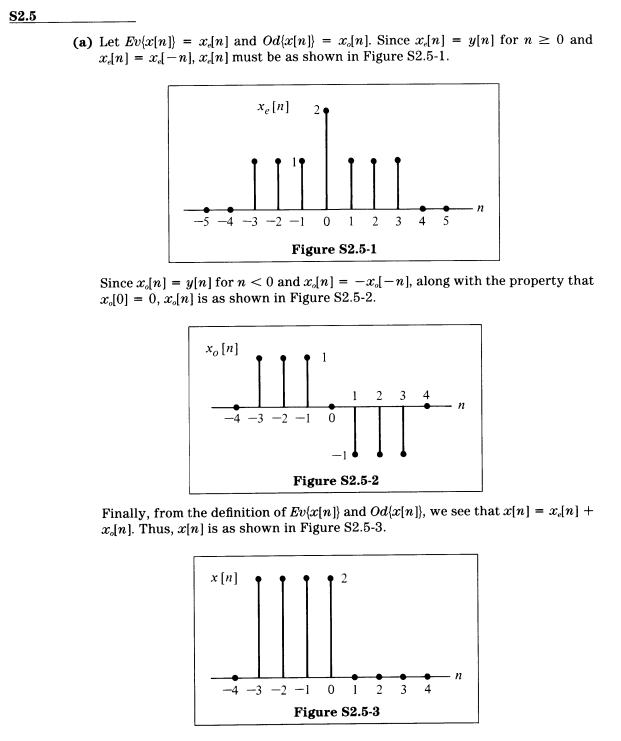
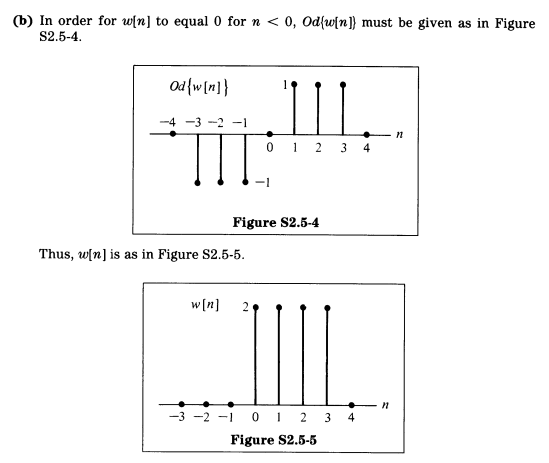
这个答案我是没怎么看懂，写一下我的解法：

(a)

\(n\geq 0\)的部分，x[n]的偶分量是y[n]，\(n\leq 0\)的部分，x[n]的奇分量是y[n]

\[x[0]=\frac{x[0]+x[0]}{2}=2\] \[x[1]=\frac{x[1]+x[-1]}{2}=1,x[-1]=\frac{x[-1]-x[1]}{2}=1\] \[x[2]=\frac{x[2]+x[-2]}{2}=1,x[-2]=\frac{x[-2]-x[2]}{2}=1\] \[x[3]=\frac{x[3]+x[-3]}{2}=1,x[-3]=\frac{x[-3]-x[3]}{2}=1\]

联立求解得：\(x[1]=x[2]=x[3]=0,x[0]=x[-1]=x[-2]=x[-3]=2\)

(b)

对于所有n，w[n]的偶分量是y[n]，\(n < 0\)时w[n]=0

\[w[0]=\frac{w[0]+w[0]}{2}=2\] \[w[1]=\frac{w[1]+w[-1]}{2}=1,w[-1]=0\] \[w[2]=\frac{w[2]+w[-2]}{2}=1,w[-2]=0\] \[w[3]=\frac{w[3]+w[-3]}{2}=1,w[-3]=0\]

联立求解得：\(w[0]=w[1]=w[2]=w[3]=2\)