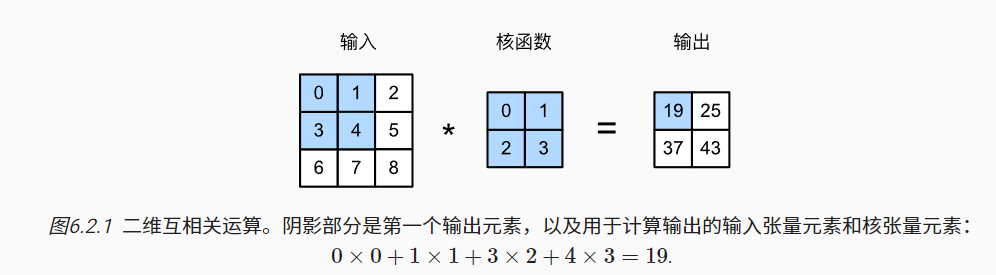
卷积

严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是互相关运算（cross-correlation）

image-20220901141420439

多输入多输出卷积

对于多输入的情况，输入是几通道卷积核就有几个通道，因为要对应通道相乘相加。

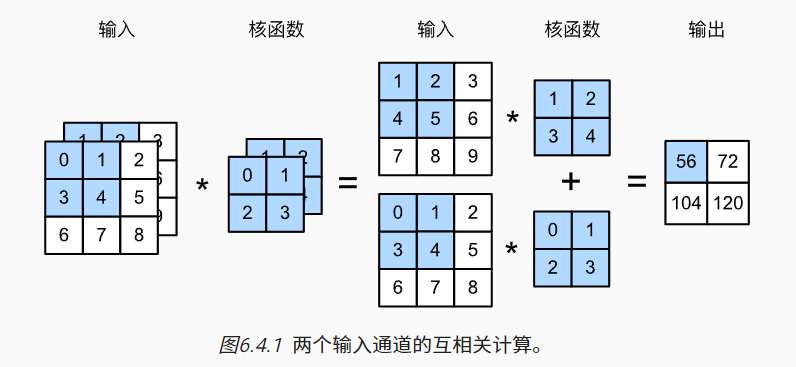
image-20220901142509173

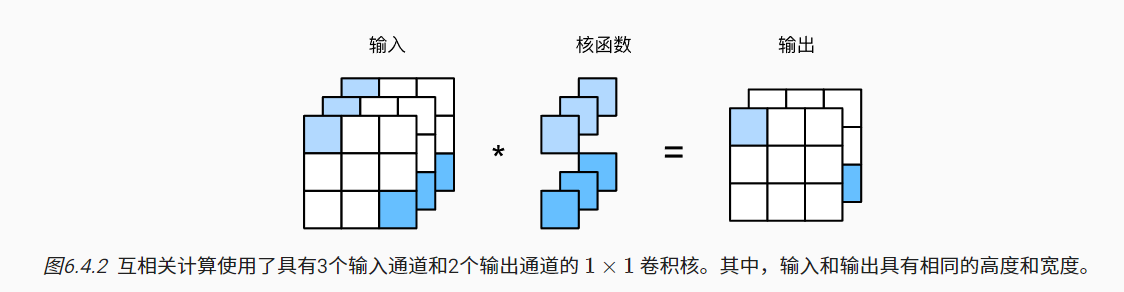
有几个输出通道就有几个卷积核。

image-20220901142524361

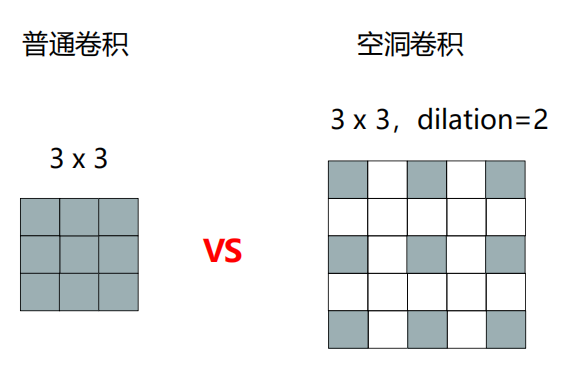
空洞卷积

image-20220901145504306

  • dilation：空洞率，空洞卷积权重值的间隔为dilation-1。

  • 当空洞率为1时，退化为普通卷积。

  • 灰色部分为卷积核权重，与左侧相同；白色部分为空，值为0

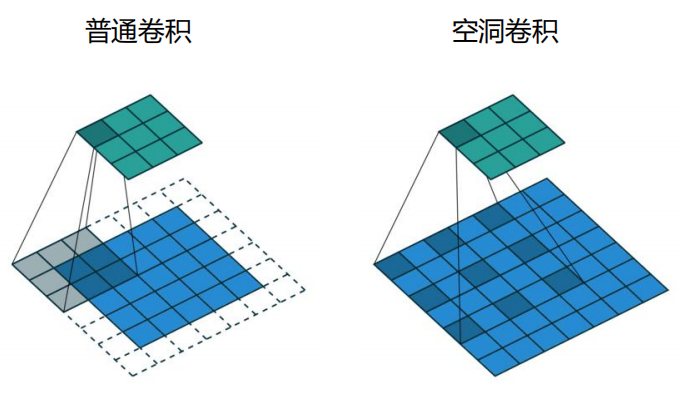
image-20220901145701402

空洞卷积感受野大小：\((k-1)*d+1\)

  • k是卷积核大小，d是dilation

Hybrid Dilated Convolution (HDC) 条件

  • 叠加卷积的 dilation rate 不能有大于1的公约数。比如 [2, 4, 6] 则不是一个好的三层卷积，依然会出现 gridding effect。
  • 我们将 dilation rate 设计成锯齿状结构，例 如 [1, 2, 5, 1, 2, 5] 循环结构。
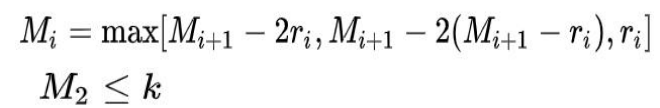
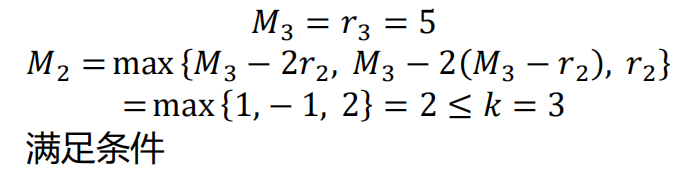
  • image-20220901161604758 image-20220901161630675 比如dilation rate [1, 2, 5] with 3 x 3 kernel就可以image-20220901161701547

size

输入大小：\(W*H\)

卷积核大小：\(k_w*k_h\)

输出大小：\((W-k_w +1)*(H-k_h+1)\)

padding

输入大小：\(W*H\)

卷积核大小：\(k_w*k_h\)

padding大小：\(p_w*p_h\)

通常，如果我们添加\(p_h\)行填充（大约一半在顶部，一半在底部）和\(p_w\)列填充（左侧大约一半，右侧一半），则输出形状将为

\[(W-k_w+p_w+1)*(H-k_h+p_h+1)\]

这意味着输出的高度和宽度将分别增加\(p_h\)和\(p_w\)。

在许多情况下，我们需要设置\(p_h=k_h−1\)和\(p_w=k_w−1\)，使输入和输出具有相同的高度和宽度。 这样可以在构建网络时更容易地预测每个图层的输出形状。假设\(k_h\)是奇数，我们将在高度的两侧填充\(p_h/2\)行。 如果\(k_h\)是偶数，则一种可能性是在输入顶部填充\(⌈p_h/2⌉\)行，在底部填充\(⌊p_h/2⌋\)行。同理，我们填充宽度的两侧。

卷积神经网络中卷积核的高度和宽度通常为奇数，例如1、3、5或7。 选择奇数的好处是，保持空间维度的同时，我们可以在顶部和底部填充相同数量的行，在左侧和右侧填充相同数量的列。

此外，使用奇数的核大小和填充大小也提供了书写上的便利。对于任何二维张量X，当满足： 1. 卷积核的大小是奇数； 2. 所有边的填充行数和列数相同； 3. 输出与输入具有相同高度和宽度 则可以得出：输出Y[i, j]是通过以输入X[i, j]为中心，与卷积核进行互相关计算得到的。

stride

输入大小：\(W*H\)

卷积核大小：\(k_w*k_h\)

stride大小：\(s_w*s_h\)

输出大小：\(\frac{W-k_w+s_w+1}{s_w}*\frac{H-k_h+s_h+1}{s_h}\)

既有padding又有stride

输入大小：\(W*H\)

卷积核大小：\(k_w*k_h\)

stride大小：\(s_w*s_h\)

padding大小：\(p_w*p_h\)

输出大小：\(\frac{W-k_w+p_w+s_w+1}{s_w}*\frac{H-k_h+p_h+s_h+1}{s_h}\)

带空洞卷积的卷积

输入大小：\(W*H\)

卷积核大小：\(k_w*k_h\)

dilation：\(d\)

先计算空洞卷积的感受野： \(k_w*k_h = ((k_w-1)*d+1)*((k_h-1)*d+1)\)

然后再把感受野带入后续的计算，感受野就是之前的卷积核大小。没有空洞卷积的时候，感受野=卷积核面积，有空洞卷积的时候要按上个式子计算。

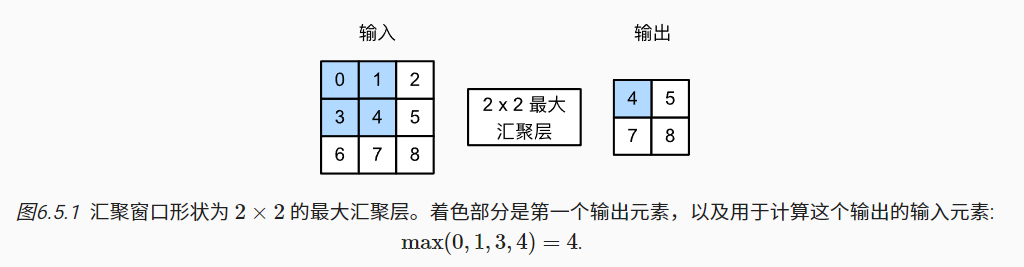
池化

目的：降低卷积层对位置的敏感性，同时降低对空间降采样表示的敏感性。

不同于卷积层中的输入与卷积核之间的互相关计算，池化层不包含参数。 相反，池运算是确定性的，我们通常计算池化窗口中所有元素的最大值或平均值。这些操作分别称为最大池化层（maximum pooling）和平均池化层（average pooling）。

在处理多通道输入数据时，池化层在每个输入通道上单独运算，而不是像卷积层一样在通道上对输入进行汇总。 这意味着池化层的输出通道数与输入通道数相同。

池化的输出计算和卷积层是一样的

输入大小：\(W*H\)

池化核大小：\(k_w*k_h\)

stride大小：\(s_w*s_h\)

padding大小：\(p_w*p_h\)

输出大小：\(\frac{W-k_w+p_w+s_w+1}{s_w}*\frac{H-k_h+p_h+s_h+1}{s_h}\)

image-20220901140753329