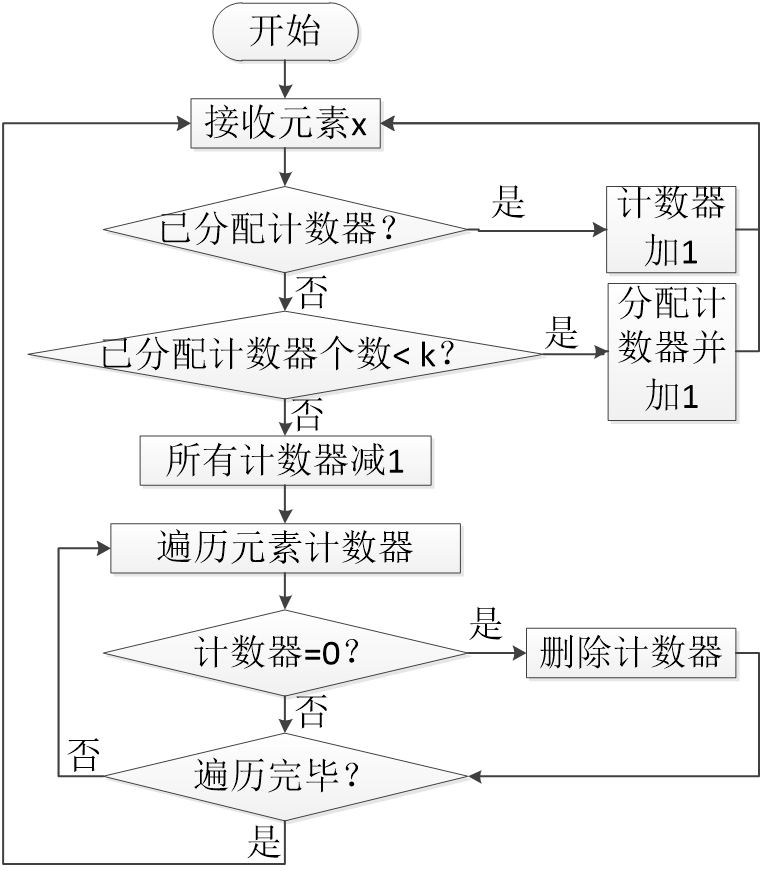
Misra-Gries算法求最频繁项

发生减法的轮数

当内存中计数器都用完之后，才会出现计数器减一的操作。此时，计数器值共减少k，包括被舍弃的新数据项，计数器值之和共比实际到达的数据项的个数少k+1。

设n是数据流中所有元素出现的次数，n’是当前所有计数器之和。计数器减1的操作有\(\frac{n-n'}{k+1}\)次（总共减少的数目除以一次减少的数目，结果就是有多少次）。若最后的计数器值之和是大于等于0的，计数器减一的操作最多执行了\(\frac{n}{k+1}\)轮。

正确性

数据流中有n个数，每个数\(n_i\)对应的频次为\(f_i\)

当 最频繁项的频次<发生减法的轮数 时， 数据可能丢失

最多减少了\(\frac{n}{k+1}\)轮

当\(f_i>\frac{n}{k+1}\)时，数据就不会丢失了。

即\(k+1>\frac{n}{f_i}=\frac{1}{ϕ}，ϕ是频率\)，Misra-Gries是一个准确的算法。