h=0.1，x是要估计的，已知x只可能发+10或-10及概率，\(w[n]\sim N(0,1)\)，接收到的信号是y[n]=0.5

问题：如何估计x[n]？

方法：ML、MAP

1、先验概率不同，p(x=+10)=0.2,p(x=-10)=0.8

ML：

\[\text { 似然函数: } p(y(n) \mid x(n))=\left\{\begin{array}{l} \frac{1}{\sqrt{2 \pi}} e^{-\frac{(y(n)-1)^{2}}{2}}=0.35, x(n)=+10 \\ \frac{1}{\sqrt{2 \pi}} e^{-\frac{(y(n)+1)^{2}}{2}}=0.13, x(n)=-10 \end{array}\right.\]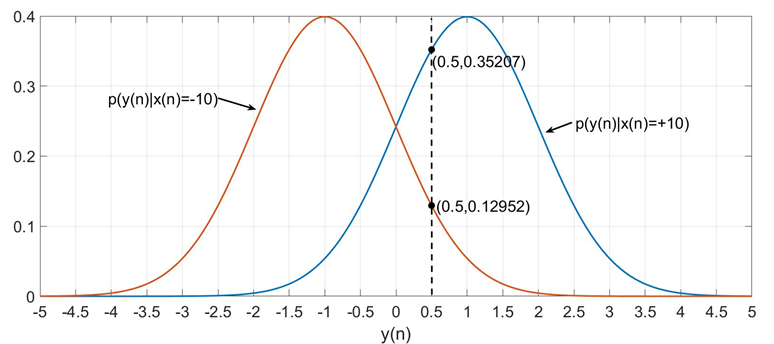

判x[n]为+10

MAP

\[\begin{aligned} &\text { 后验概率 } \\ &p(x(n) \mid y(n))=p(x(n)) f(y(n) \mid x(n))= \begin{cases}0.2 \times \frac{1}{\sqrt{2 \pi}} e^{-\frac{(y(n)-1)^{2}}{2}}=0.07, & x(n)=+10 \\ 0.8 \times \frac{1}{\sqrt{2 \pi}} e^{-\frac{(y(n)+1)^{2}}{2}}=0.10, & x(n)=-10\end{cases} \end{aligned}\]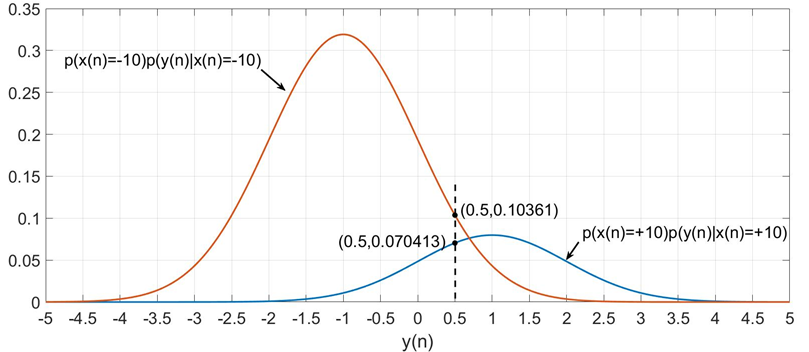

判x[n]为-10

2、先验概率相同，p(x=+10)=0.5,p(x=-10)=0.5

ML与MAP等价

判x[n]为+10